为什么会存在二八法则决定论
话说自从牛顿力学被提出后,经过物理学家和数学家的深化和发展。当时的人们开始能够很好地预测各种现象。其中有个叫做拉普拉斯的科学家提出了一个思想实验:拉普拉斯妖。
这个思想实验可是相当了不得,他和芝诺的乌龟、麦克斯韦的妖以及薛定谔的猫并称为科学史上的四大神兽,无论哪个都是科学家花了很长时间才能迈过的坎。当然,薛定谔的猫还没成功解释。

拉普拉斯认为宇宙现在的状态其实就是因为过去的状态导致的,而未来的状态则是由现在的状态导致的。如果有一个智者(拉普拉斯妖)知道某一个宇宙中所有的力和物体的位置,并且它能够瞬间完后才能对这些数据的分析,那么从最小的粒子到最大的物体,它们的运动都会被包含在一条简单公式里,他就可以预测任意时刻宇宙万物的变化。
后来,科学家们管这种思考方式叫做:决定论。

概率描述的世界
不过好景不长,100多年后量子力学诞生,人们发现拉普拉斯妖根本不可能做到预测万物的事。
首先是在微观世界,有个量子力学的测不准原理守着,这个定理告诉我们,我们不可能同时测量出一个粒子的动量和位置,不是因为仪器不行,而是观测了动量,就测不准位置,观测了位置,就测不准动量。
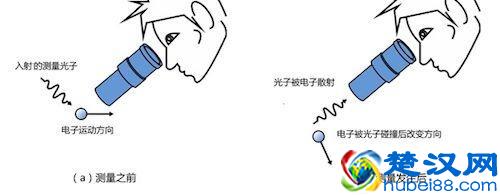
这时候科学家才意识到,在微观世界离,我们只能依靠概率来描述。就比如说,氢原子核外的电子,我们只能用概率云来描述。

然而仅仅是这样么?
没多久,宏观世界的预测也被打破了。而打破这个的叫做:混沌现象。
我们更熟悉另个外号:蝴蝶效应。这是指在一个动态系统里,只要初始条件发生微小变化,就会带动整个系统长期且巨大的链式反应。
还有一个很通俗的版本:一只蝴蝶在巴西轻拍翅膀,可以导致一个月后德克萨斯州的一场龙卷风。

而且科学家发现,其实混沌系统无处不在,我们的社会,股市其实都是一个超级复杂的混沌系统。而混沌系统受到初始条件的影响很大,初始条件稍微改变一下就会千差万别。
最简单的混沌系统应该就是双摆了。如果一开始有一点点微小的不同,摆杆的轨迹就会完全不一样。

不确定性原理和混沌系统告诉我们一个道理,以往研究对象其实都是线性的。说白了,就是很好找到因果关系或者相关关系,这也是决定论能够成立的原因。
但这个世界,存在更多的是非线性的系统,这个系统超级复杂,已经远远超过人类的算力,我们是不可能用几个简单公式就能直接描述的。我们能描述的仅仅是概率罢了。
正态分布科学家就曾尝试用概率分布来分析整个系统,比如:正态分布。它的样子很像一个倒扣的钟。所以也叫做:钟形曲线。
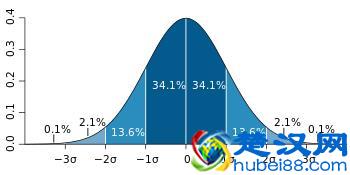
这种分布其实是常用在离散模型当中,比较常见的就是高尔顿板。
如果搞一块竖直放置的板,在上面钉上交错排列的钉子。让小球从上端自由下落,这个时候,小球碰到钉子就会随机向左或者向右落下。这时候,我们得到的就会是一个正态分布。而每个豆子之间是相互独立的。

除了高尔顿板,我们还常常需要描述一个班级的女生或者男生的身高,这也是一个很标准的正态分布。但是我们知道,其实每个同学的身高也是相互独立。
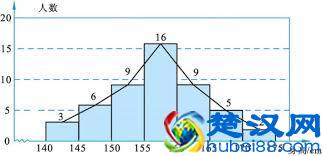
幂律分布
除了正态分布,这世界上还存在着另外一个更为常见,但高中和大学都不会学到的分布:幂律分布。幂律分布比起正态分布,其实更和我们生活息息相关。
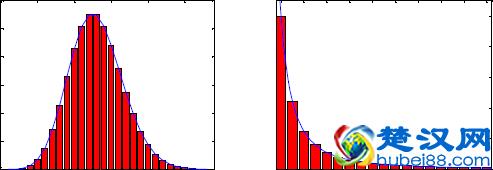
坐:正态分布;右:幂律分布
讲幂律分布之前,我们先来讲一个沙堆效应。玩沙堆基本上是每个人的童年都玩过的。
当沙堆堆到一定程度时,我们继续一颗一颗地放沙子,根据目前的科学理论,我们无论如何也不能够预测得了放到哪一颗沙子时,沙堆会垮掉。
因为它实在是太复杂了,内部每一颗沙子之间都在相互作用。
实际上,我们的社会就是这样,每一个人都紧密联系。甚至到了近代,互联网出现之后,这个联系更加紧密。也就是说,我们每个人其实都像沙堆里的一颗沙子一样,时时刻刻在相互作用,而不是相互独立的,所以,描述很多人类社会的问题,用正态分布是行不通的。
在这个系统中,更多的是赢家通吃,我们也管着现象叫做“二八法则”。常见的就是那句很有名的话:社会上20%的人占有80%的社会财富。
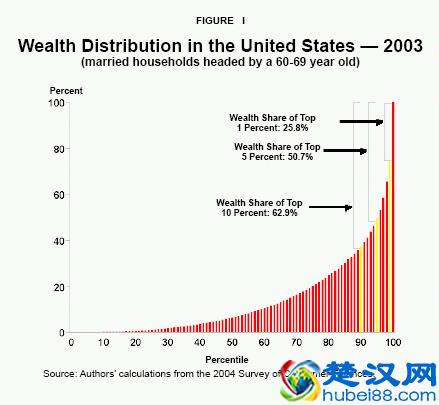
有人曾经模拟这个世界的运行规律,他们假设:每人在18岁带着100元,然后开始玩游戏。
每天就玩一次,直玩到退休(65岁)。“每天拿出一元钱”作为为日常消费随机给其他人,并设定了获得财富的概率随机。
一个人一生要玩大概17000次游戏,也就是说会获得17000次财富分配的机会。
那结果会如何呢,很多人都参与了,猜测结果大概有以下三种
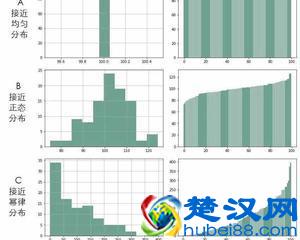
来源:城市数据图
结果呢?电脑模拟结果其实是幂律分布。
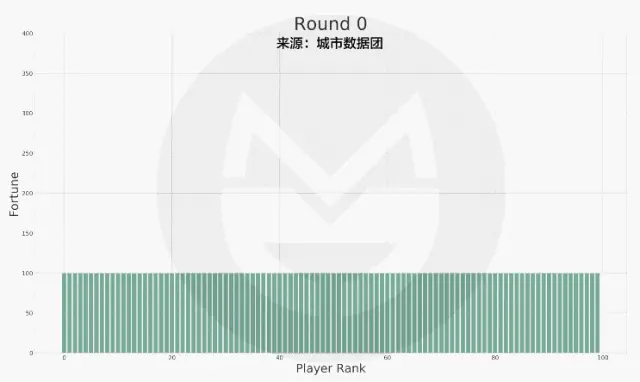
来源:城市数据图
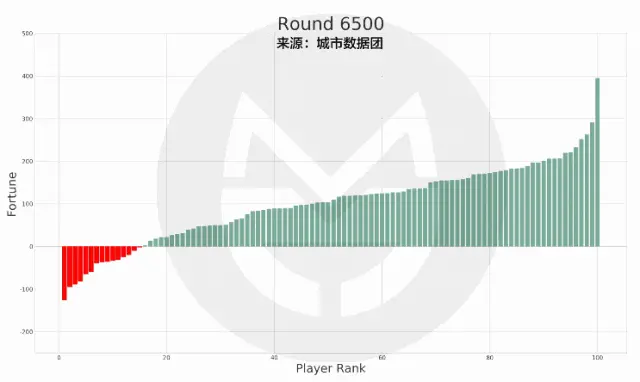
这个允许负债的结果;来源:城市数据图
所以相互紧密联系和充分竞争的系统中,正态分布其实并不适用,我们要用幂律分布的思维方式去思考。如果我们想尝试用决定论的方法去解决很多这类问题,你会发现根本做不到。很多事情,比如:世界大战,股市涨跌等其实都不能用单一因素来解释,因为它压根就是非线性的系统。
那我们如何才能成为二八法则中的那个20%呢?
本文地址:问答解惑频道 https://www.hkm168.com/live/125656.html,易企推百科一个免费的知识分享平台,本站部分文章来网络分享,本着互联网分享的精神,如有涉及到您的权益,请联系我们删除,谢谢!



 相关阅读
相关阅读